[청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 2편)

[서포터즈 MISSION 03. 강의노트 작성하기 2] - 반도체 물성 및 소자 2편

안녕하세요!

SK 하이닉스 청년 Hy-Po 4기 교육생이자 서포터즈 2기로 활동중인 교육생 김세영입니다!

오늘도 역시 서포터즈의 3번째 미션인 강의노트를 작성해 볼 예정입니다.😊😊

저번 1편에서 언급했다시피 내용이 많기 때문에 나눠서 작성하는 중입니다...😭

전공 과목이라서 배운 적 있는 내용이지만 그때도 어려웠는데... 지금도 어렵네요...😂😂

이번에도 역시 유도과정 등의 수식은 제외하고 개념만 담아볼 예정입니다.

바로 시작하겠습니다!!

[4️⃣ 반도체의 이해 2]

📝 [복습] 에너지상태밀도 (DOS : Density Of State)와 페르미-디락 확률함수

에너지 상태 밀도 (DOS : Density Of State) 함수
- 에너지 밴드 내 전자가 가질 수 있는 에너지 상태의 밀도
- 단위 에너지당 단위 부피당 양자 상태 수

페르미-디락 확률 함수
- 결정에서 에너지 E의 양자상태에 전자가 채워질 확률

📝 평형상태에서 반도체의 전자, 정공 분포

전도대의 전자 농도 분포

가전자대의 정공 농도 분포

반도체의 전자, 정공 농도 분포
- 평형상태의 진성반도체에서 전자농도-정공농도
- Ef는 밴드갭 (금지대) 내에 위치
- 만약 유효질량이 같다면 gc(E)와 gv(E)는 대칭 형태의 분포이고, Ef는 밴드갭의 중앙에 위치 (실제로는 유효질량이 달라 Ef가 밴드갭의 중앙에서 벗어나게 됨)

📝 반도체의 전자, 정공 농도 (n0, p0)

전자농도(n0)는 n(E)의 전도대 에너지전체에 대한 적분

정공농도(p0)는 p(E)의 가전자대 에너지전체에 대한 적분

둘은 상보적 관계에 있다.

📝 반도체의 전자, 정공 농도 (n0, p0)의 특성

반도체의 전자, 정공 농도 (n0, p0)
- Ec - Ef가 작을수록 n0가 커지고, Ef - Ev가 작을수록 p0가 커진다.
- Ec, Ev는 반도체 재료의 고유 특성이고, Ef는 경우(도핑 등)에 따라 달라진다.
- n0, p0는 서로 상보적이다.
유효상태밀도함수 (Nn, Np)
- Nn, Np를 각각 전도대와 가전자대의 유효상대밀도함수라 함.
- 온도의 영향을 받는 반도체 재료의 고유 특성
- 반도체마다 다르고 전자와 정공의 유효질량에 차이에 따라 다소 다른 값을 가진다.

📝 진성반도체의 캐리어 농도 (n0, p0)

진성 반도체 (Intrinsic semiconductor)
- 불순물과 결함이 없는 순수한 반도체 (doping이 없는 순수 반도체)
- 이때 전자, 정공농도를 ni, pi라 표기하고, ni=pi이므로 단순히 ni를 진성캐리어농도라 함
- 진성 반도체의 페르미 에너지를 진성 페르미 에너지라 하고 밴드갭의 중간에 위치
- 진성 캐리어 농도 (ni)는 반도체 재료의 고유특성 (Ef에 무관하게 일정)
- 온도에 따라 크게 변화 (고온일수록 높다)

📝 진성반도체의 페르미에너지 준위

진성반도체
- 전자의 유효질량과 정공의 유효질량이 다르면 Efi는 밴드갭의 중간에서 벗어난다
- 이때, 유효질량이 가벼운 밴드 (전도대 or 가전자대)쪽으로 가까워짐.
  이는 유효질량이 가벼운 쪽이 상태밀도함수가 적고, 그에 따라 동일 캐리어 농도를 위해 높은 확률로 전자가 채워져야(지워져야)하기 때문이다.

📝 도펀트와 도핑의 원리 : n 도핑 (전자 도핑)

→ mobile electron이 발생하는 도핑

Si 결정의 n도핑 : 정성적 설명
- 4족 원소의 Si로 이루어진 Si 결정에 5족 원소를 치환불순물로써 도입
- 5족 원소의 5개 가전자 중 4개는 실리콘 격자 내 공유결합에 참여
- 나머지 1개 전자는 매우 불안정한 상태로 5족 원소 가전자 궤도에 존재
  → 작은 열에너지에 의해 5족 원소를 벗어나 이동 가능 → 이동 전자 방생
- 남은 5족 원소는 움직일 수 없는 (+) 상태로 이온 상태
  - n 도핑 : 이동전자가 발생하는 불순물 도입 (결정 원자수에 비해 매우 소수)
  - 도너 (donor) : 이동전자를 발생시키는 불순물
  - 고정 (+) 이온 : 전자를 내어준 donor 원자
  - 이온화 : 도너가 전자를 잃고 이온이 되는 과정
  - 이온화 에너지 : 도너의 가전자가 벗어나는 데 필요한 에너지
Si 결정의 n 도핑 : 에너지에 기반한 설명
- 4족 원소인 Si로 이루어진 Si 결정에 5족 원소를 치환불순물로써 도입
- 전도대 바닥에 매우 가까운 도너 에너지상태 발생
- 전자의 열에너지에 의해 손쉽게 돈너에서 전도대로 전자 이동
- 전자를 잃는 도너 상태는 고정된 양(+)이온화

📝 도펀트와 도핑의 원리 : p도핑 (정공(hole) 도핑)

Si 결정의 p 도핑 : 정성적 설명
- 4족 원소인 Si로 이루어진 Si 결정에 3족 원소를 치환불순물로써 도입
- 3족 원소의 3개 가전자 모두 실리콘 격자 내 공유결합에 참여
- 나머지 1개의 격자 공유결합은 전자 1개가 모자란 매우 불안정한 상태
  → 작은 열에너지에 의해 주변 Si 결정의 가전자가 이동 → 정공 발생
- 남은 3족 원소는 움직일 수 없는 (-) 상태로 이온 상태
  - p 도핑 : 정공을 발생하는 불순물 도입
  - 억셉터 (acceptor) : 정공을 발생시키는 불순물
  - 고정 (-) 이온 : 전자를 얻은 억셉터 원자
  - 이온화 : 억셉터가 전자를 얻어 이온이 되는 과정
  - 이온화 에너지 : 억셉터가 결정의 가전자를 얻는데 필요한 에너지
Si 결정의 p 도핑 : 에너지에 기반한 설명
- 4족 원소인 Si로 이루어진 Si 결정에 3족 원소를 치환불순물로써 도입
- 가전자대 끝에 매우 가까운 억셉터 에너지 상태 발생
- 전자의 열에너지에 의해 손쉽게 가전자대에서 억셉터로 전자이동 → 정공발생
- 전자를 얻은 억셉터 상태는 고정된 음(-) 이온화

📝 외인성 반도체 (extrinsic semiconductor) : 전자와 정공의 평형상태 분포

외인성 반도체 : 도핑에 의해 캐리어 농도가 조절된 반도체
- n0 != p0
- 전자가 많아지면 정공농도가 억제됨. 정공이 많아지면 전자농도가 억제됨
- 상대적으로 많은 캐리어를 다수 캐리어 (majority carrier), 적은 캐리어를 소수 캐리어 (minority carrier)
- 상태밀도함수는 결정 격자의 함수로 일정
  페르미-디락 확률함수 형태로 동일, Ef만이 이동

📝 외인성 반도체 (extrinsic semiconductor) : n0p0 곱에 대한 고찰

n0p0 = ni^2
도핑에 무관하게, 즉 전자/정공 농도에 무관하게 두 캐리어 농도의 곱은 항상 같고, 크기는 진성캐리어 농도의 제곱
n0p0 = ni^2 를 유지하며, 다수 캐리어가 소수 캐리어의 수를 억제하여 균형을 맞춤
why? 전자의 농도를 높이면 정공의 농도는 억제?
- 전자의 농도가 올라갈수록 정공과 만나 재결합할 가능성이 높다.
- 결국, 정공의 농도는 억제된다 (만날 확률이 높다)

📝 축퇴 (degenerated)와 비축퇴 (nongenerated) 반도체

비축퇴 반도체
- 일반적으로 도핑 농도를 가진 반도체에 해당
- 페르미에너지가 밴드갭의 중간 정도에 위치
- 도핑 에너지 상태들이 서로 상호작용(중첩)하지 못하고 독립적으로 존재

축퇴 반도체
- 아주 높은 도핑 농도를 가진 반도체에 해당
- 페르미 에너지가 Ec 혹은 Ev에 매우 근접
- 도핑 에너지 상태들이 서로 상호작용(중첩)하여 밴드 형성 → 반도체의 밴드가 넓어지고 밴드갭이 작아지는 형성 발생
- 페르미 에너지가 넓어진 밴드에 의해 Ec 또는 Ev 내부에 존재 → 매우 높은 전자 또는 정공 농도 (전도체처럼 동작)

📝 완전 이온화 동결

완전 이온화
- 도핑 원소의 이온화 에너지가 상온의 kT에 준하거나 작아서, 모든 도핑 원소가 이온화되어 캐리어를 발생하는 상태
- 즉, 도핑농도 = 다수캐리어 농도
  - n 도핑 : Nd = n0
  - p 도핑 : Na = p0
- 잘 정립된 반도체와 도펀트는 이에 해당

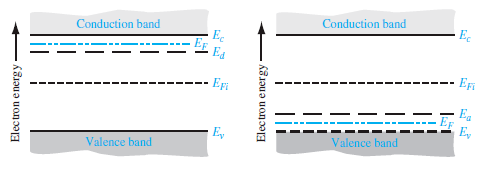
동결
- T = 0K에서 전자의 열에너지가 0eV 이므로, 도펀트들은 이온화 할 수 없음
- 이때 페르미 에너지의 위치가
  - n 도핑의 경우 : Ec와 Ed의 사이
  - p 도핑의 경우 : Ea와 Ev의 사이
  - 에 위치함으로써 앞선 캐리어 농도 이론과 동일하게 적용 가능

📝 보상 (compensated) 반도체

보상 반도체 : n 도펀트와 p 도펀트가 모두 있는 반도체
- n 도핑과 p 도핑이 서로 상쇄하여 보다 높은 도핑 농도가 다수캐리어 형성
보상 반도체 내 캐리어 농도의 통계적 표현
- 임의의 반도체에서 순전하량은 중성(0)이다
- 보상 반도체에서 완전 이온화를 가정하면 음전하량 = 양정하량

📝 온도와 도핑 및 캐리어 농도의 관계

매우 저온에서는 kT < Ec - Ed 즉, 전자의 열에너지가 도펀트의 이온화 에너지보다 작으므로 도핑 효과 감소
중간정도의 온도 (일반적으로 반도체 사용온도)는 도펀트가 완전 이온화되어, 도핑을 통해 외인성 반도체의 특성 조절 가능
매우 고온에서는 진성 캐리어 농도가 증가하여 도핑농도보다 높아지므로, 도핑에도 불구하고 진성반도체의 특성을 가짐

[5️⃣ 캐리어 전송현상]

📝 드리프트 전류 (drift current)

드리프트 전류
- 전기장이 걸리면 모바일 캐리어 (전자, 정공)이 쿨롱힘에 의해 이동함으로써 전기장 방향의 전류 발생
- 정공(+) 이동방향 = 정공 드리프트 전류 방향 = 전기장 방향
- 전기장 방향 = 전자 드리프트 전류 방향 (전자의 이동방향과 반대)
- 평균 드리프트 속도를 vd라고 하고 양의 전하밀도를 p라고 하면, 드리프트 전류밀도는 J = pvd

📝 캐리어 드리프트에 대한 고찰

고전역락에 의한 정공 움직임의 예상
- 쿨롱힘에 의해 가속
고체 내에서 전기장에 의한 캐리어의 드리프트 전도 모델
- 전기장에 의해 가속
- 결정 격자 또는 이온화된 불순물에 의해 산란 (scattering)
- 산란 시 거의 멈춘 상태에서 전기장에 의해 재가속
실제 고체 내 캐리어의 움직임
- 전자는 매우 빠르게 무작위 열운동
- 고체 내 산란에 의해 바른 랜덤 운동
- 전기장 인가 시, 쿨롱힘에 의해 랜덤 운동에 전기장 방향 경향성 발생

📝 산란에 의한 충돌평균시간과 이동도

전기장에 의한 드리프트 속도는 무작위열속도에 비하면 매우 작음
전자의 캐리어의 총속도는 드리프트 속도에 무관하게 일정하고 따라서 충돌평균시간이 전기장에 무관하게 동일
결국, 캐리어의 드리프트는 충돌평균시간 동안만 전기장에 의해 가속되는 운동
이동도는 충돌평균시간에 정비례함.
충돌평균시간 (mean free time)을 결정하는 요소는 drift가 아니라 총 속도 그래서 거의 constant하다

📝 온도, 도핑 농도에 따른 이동도 (산란의 이해 지배)

온도가 상승하면, 격자산란과 이온불순물산란이 증가하여 이동도가 감소
도핑이 증가하면, 이온불순물 산란이 증가하여 이동도 감소
이동도를 저하하는 여러 요인이 있을 대, 가장 크게 저하하는 요인이 이동도를 좌우
비정질이냐, 단결정이냐에 따라서도 달라짐.

📝 속도 포화

전기장 크기가 증가할 경우, 캐리어의 드리프트 속도는 무한정 증가할 수 없고 포화된다.
- 위 식에서 캐리어의 드리프트 속도는 비례상수 이동도에 의해 전기장에 따라 증가
- 이는 드리프트 속도가 무작위열속도보다 매우 느려서 충돌평균시간이 전기장에 무관하게 일정하는 가정 하에 성립
- 하지만, 매우 높은 전기장의 경우, 캐리어의 드리프트 속도가 무작위 열속도 10^7cm/sec 수준에 달하고, 이 경우 전자의 총 속도가 증가하여 충돌평균시간이 감소
- 결국, 매우 높은 전기장에서는 이동도가 감소하고 전기장 증가를 상쇄하여 일정한 드리프트 속도에 포화됨.
  이는 전기장이 증가해도 드리프트 전류가 증가하지 않고 포화됨을 의미함

📝 입자의 확산과 확산전류 (diffusion current)

확산 (diffusion)
- 무작위 열 운동하는 입자는 농도가 높은 위치에서 낮은 위치로 확산한다.
확산 전류 (diffusion current)
- 고체 내에서 캐리어 농도가 일정하지 않으면 (구배가 있으면) 농도가 높은 곳에서 낮은 곳으로 확산 이동하고, 전하를 띤 입자(캐리어)의 이동은 전류가 발생한다.

전자는 농도가 높은 곳에서 낮은 곳으로 흐르고 전자의 이동과 전류의 방향은 반대이므로, 전자확산전류의 방향은 전자농도 구배와 같은 방향
정공은 농도가 높은 곳에서 낮은 곳으로 흐르고 정공의 이동과 전류의 방향은 동일하므로, 정공확산전류의 방향은 정공농도 구배와 반대 방향
확산 전류는 캐리어 농도의 변화량과 확산계수에 비례

📝 반도체의 총 전류밀도

반도체에는 4개의 독립된 전류 성분이 존재
- 전자 드리프트 전류
- 정공 드리프트 전류
- 전자 확산 전류
- 정공 확산 전류
드리프트 전류 개요
- 전기장에 의한 캐리어의 드리프트 이동에 의해 발생
- 전기장과 동일 방향 (전자, 정공 동일)
- 전기장에 정비례 (비례상수 : 이동도)
- 캐리어 농도에 정비례
확산 전류 개요
- 캐리어 농도 구배에 의한 캐리어의 확산 이동에 의해 발생
- 전자는 농도 구배와 동일 방향, 정동은 농도 구배의 반대방향
- 캐리어 농도 구배(변화량)에 정비례 (비례상수 : 확산계수)
반도체의 총 전류밀도

📝 비균일 도핑농도의 외인성 반도체

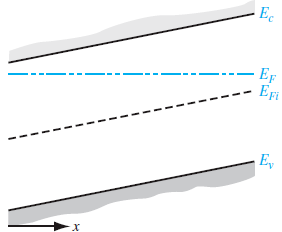
열평형 상태에서의 반도체와 전도체 - 균일 페르미 에너지
- 상호 간 캐리어 이동이 가능한 반도체, 전도체로 구성된 구조의 전체 영역에서 페르미에너지가 동일
- Ef는 고체 내에서 전자 기준 캐리어의 평균 에너지이고, Ef가 높은 곳으로 낮은 곳으로 전자가 확산이동하여 결국 모든 영역에서 Ef가 동일하게 맞춰짐
- 자세하게는, 전자 또는 정공 이동에 의해 전하량 분포가 발생하고, 이에 의한 전기장(전위차)으로 인해 Ef가 동일하게 맞춰짐
열평형 상태에서의 반도체 - 전류 관점
- 외부 전압이 없을 때 순 전류 0
- 외부 전압이 없으면, 반도체 내부에 흐르는 전류는 0이 되어야 함
- 비균일 도핑된 반도체는 캐리어 농도 구배 존재 → 확산 전류가 발생 → 고정이온(도펀트)과 캐리어 간 농도 불일치에 의한 공간전하 발생 → 전기장 발생 → 드리프트 전류 발생 → 확산전류 상쇄 → 순-전류 0

[6️⃣ 반도체의 비평형상태]

📝 평형상태 (equilibrium state) or 열적평형상태

평형상태 (equilibrium state) or 열적평형상태
- 반도체의 모든 위치가 동일 온도를 가지고, 그 외 외부로부터 자극이 없는 상태 (외부자극의 예 : 금속 온도 변화, 외부로부터의 전압 차, 빛 등)
- 만약 외부자극에 의해 비평형상태가 되더라도 더 이상의 자극이 없으면 평형상태로 돌아감
- 이때의 캐리어 농도를 n0, p0라 함
평형상태의 전자-정공 생성 / 재결합
- 전자-정공 생성
  - 가전자대의 전자가 전도대로 여기됨으로써 전자-정공 쌍 발생
- 전자-정공 재결합
  - 전도대의 전자가 가전자대의 빈 준위상태를 만나면 가전자대로 떨어지는 현상
  - 즉, 전자와 정공이 만나서 재결합 → 전자-정공 쌍 소멸
- 가전자대의 전자는 열적 과정의 무질서함에 의해 끊임없이 전자-정공 생성, 동시에 끊임없이 만나 전자-정공 재결합 발생
- 평형상태에서 캐리어 농도 일정 ← 생성률 = 재결합률

📝 과잉 캐리어 재결합률

과잉캐리어는 시간에 따라 감소하여 사라짐 → 캐리어 농도는 평형 상태로 돌아감
이때 외인성 반도체의 저-수준 주입 조건이면, 다수 캐리어의 농도는 거의 불변, 소수 캐리어의 농도만 변화
시정수를 과잉 소수 캐리어 수명이라고 하고, 다수 캐리어 농도에 반비례
과잉 캐리어의 재결합률은 과잉 캐리어의 농도와 다수 캐리어의 농도에 비례
과잉 전자와 과잉 정공의 농도는 독립적이지 않고, 동일 양과 비율로 변화

📝 과잉 캐리어의 특성 : 전송현상

평형 상태 반도체 내 캐리어의 전송
- 전자와 정공이 전기장의 방향과 각각의 농도 구배 방향에 대해 독립적으로 움직임
비평형상태 반도체 내 과잉 캐리어의 전송
- 과잉 전자와 과잉 정공이 반대방향으로 움직이면, 내부 전계가 발생 → 과잉 전자와 과잉정공 사이에 인력발생 → 떨어지지 못하고 함께 움직임
- 이를 앰비폴러 전송 (ambipolar transport)라 함

📝 과잉 캐리어의 전송의 이해 : 앰비폴러 전송

과잉 전자 과잉 정공 쌍과 내부 전기장
- 만약 외부전기장에 의해 과잉 전자와 과잉 정공이 반대방향으로 움직이면, 전하 분포에 의한 내ㅜㅂ 전기장 발생
전자 - 정공 쌍의 생성과 재결합은 항상 쌍으로 발생한다.

📝 앰비폴러 전송의 응용

전자와 정공을 따로 넣어도 동작은 동일

위치 x=0에서 과잉 캐리어가 발생하고, 외부 전계 인가가 없을 때, 시간에 따른 정공 농도 분포
확산 + 재결합 (생성은 제외하고 고려함)

위치 x=0에서 과잉 캐리어가 발생하고, 외부 전계 인가가 있을 때, 시간에 따른 정공 농도 분포
확산 + 드리프트 + 재결합

📝 유사-페르미 (Quasi-Fermi) 에너지 준위

평형 반도체에서 페르미 에너지 준위
- 전자와 정공이 하나의 페르미 에너지를 가진다.

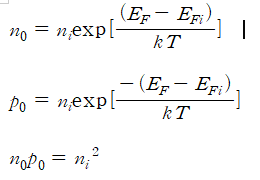
비평형 반도체에서 페르미 에너지 준위
- 전자와 정공이 각각의 페르미 에너지를 가진다.

이렇게 해서 반도체 물성 및 소자 2편 정리가 끝났습니다!!

처음에 전공 수업을 들었을 때도 느꼈지만... 정말 양이 너무 많은 것 같아요...

3편으로 정리를 다 할 수 있을지 의문이네요...😭😭😭

꾸준히 공부하는 습관, 꾸준히 기록하는 습관을 들이려고 노력을 많이 하는 중인데 열심히 하고 있는건지 잘 모르겠어요...

그래도 꾸준히! 성실하게! 하려고 많은 노력을 하고 있습니다.

단기적인 목표를 말씀드리자면 저는 이번 하이포 활동이 끝나기 전까지 공정 파트 정리까지 끝내는 것이 개인적인 목표랍니다...ㅎㅎ

할 수 있겠죠...?🤔🤔🤔🤔🤔

그래도 뭐... 어쩌겠어요 해야지😉

저는 그럼 다음 편인 반도체 물성 및 소자 3편으로 다시 돌아오겠습니다!!

다음편도 기대해주세요!😘😘😘

출처 :

Introduction to Semiconductor Devices, Neamen, McGraw-Hill

Semiconductor Physics And Devices, Neamen, McGraw-Hill

https://cucudasdiary.tistory.com/33

https://hj-everything.tistory.com/54

http://contents.kocw.or.kr/KOCW/document/2015/chungnam/kimdongwook/11.pdf

리드미 링크 : https://www.leadme.today/5801808498262016

(※ 본 게시물은 청년 Hy-Po 서포터즈 2기 활동의 일환으로 작성되었습니다.)

LIST

'대외활동 > SK하이닉스 청년 Hy-Po 4기' 카테고리의 다른 글

[청년 Hy-Po 서포터즈 2기] - MISSION 05. 강의노트 작성하기 3 (반도체 물성 및 소자 3편) (1)	2024.02.12
[청년 Hy-Po 서포터즈 2기] - MISSION 04. 자유주제 (나의 경험 공유) (1)	2024.02.04
[청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 1편) (1)	2024.01.28
[청년 Hy-Po 서포터즈 2기] - MISSION 02. 청년 하이포리얼리즘♡ (2)	2024.01.21
[청년 Hy-Po 서포터즈 2기] - MISSION 01. 강의노트 작성하기 (회로이론) (1)	2024.01.14

PORTFOLIO_SY