반응형
[서포터즈 MISSION 05. 강의노트 작성하기 3] - 반도체 물성 및 소자 3편
안녕하세요!
SK 하이닉스 청년 Hy-Po 4기 교육생이자 서포터즈 2기로 활동중인 교육생 김세영입니다!
5번째 미션은 바로 강의노트 작성하기 3편입니다!
저번 강의노트 작성하기 2편에서 다 작성하지 못한 부분들 부터 최대한 제가 작성할 수 있는 곳 까지 정리하면서 복습을 진행해볼 예정입니다.
이번에도 역시 유도과정 등의 수식은 제외하고 개념만 담아 정리할 예정입니다.
바로 시작할까요?
[6️⃣ PN 정션 1]
📝 다이오드의 특성 개요


- 다이오드 (Diode)
- 저항과 같이 전압이 걸리면 전류가 흐르는 2단자 소자
- 양극 (anode), 음극 (cathode)
- 어원 : 이극 진공관 (cf. 트라이오드 : 삼극 진공관)
- 양극 기준 순방향 전압 (forward bias)에만 전류가 흐르고, 역방향 전압 (backward bias)에는 전류가 흐르지 않는다.
- 즉, 역방향 전압에 대해 매우 높은 저항
- 순방향 전압에서 전류가 흐르기 시작하는 문턱전압 (threshold voltage, Vt) 존재
역방향 전압에서 전류가 흐르기 시작하는 (소자가 파괴되는) 파괴전압 (breakdown voltage) 존재
- 저항과 같이 전압이 걸리면 전류가 흐르는 2단자 소자
📝 PN 접합의 기본구조 및 반도체의 기본 거동
- PN 정션에서 반도체의 정성적 거동
- p영역의 정공이 n영역으로 확산
n영역의 전자가 p 영역으로 확산 - p영역에 억셉터 도펀트에 의한 (-) 공간전하 발생
n영역에 도너 도펀트에 의한 (+) 공간전하 발생 - 공간전하에 의한 n영역 → p영역 전기장 발생
- 균형
- 공간전하영역 외부 p영역, n영역으로부터 캐리어 확산력 = 공간전하영역 내부의 전계력
- 공간전하영역 외부 p영역, n 영역으로부터의 캐리어 확산 = 공간전하영역 내부의 전계력에 의한 캐리어 드리프트
- p영역의 정공이 n영역으로 확산
📝 PN 접합 정상상태 ( "zero" voltage bias )
- 에너지밴드 다이어그램 : 반도체 소자의 정성적 이해에 매우 강력(필수적인) 툴

- 에너지밴드 다이어그램 그리기
- 정션 발생 전, 각 영역의 본질적인 에너지밴드다이어그램 파악
- 정션 발생 시, 0 bias의 열평형을 고려 → 균일한 fermi level → fermi level을 기준으로 에너지밴드 다이어그램 그림
- fermi level을 기준으로 정션에서 충분히 먼 영역은 위 1의 에너지밴드와 동일
- 정션 부분은 위 3의 에너지밴드를 자연스럽게 이어지도록 제작
- 2에서 0 bias의 열평형 조건에 주의
- 3에서 충분히 먼 영역은 공핍층 이상의 먼 영역을 의미
- 4에서 자연스럽게 이어가는 형태는 전자재료의 종류에 따라 다름

- 주요 파라미터
- 내부 전위장벽 (built in potential)
- 공간전하폭 (space charge width, depletion width)
- 내부 전하량 분포, 전계, 전위
- 내부 전위장벽
- PN 접합의 정상상태에서 전하 분포에 의한 에너지밴드 밴딩으로 발생하는 전위차
- 전자의 n 영역 → p영역 확산 이동과 정공의 p영역 → n영역 확산이동에 대한 장벽으로 작용하여 균형을 유지
(p와 n영역 끝부분에서 "확산전류 = 드리프트 전류"와 동일 의미)
- 내부 전위장벽의 계산
- "전하량 분포 → 전계분포 → 전위분포"로 부터 구할 수 있음
- 또는, 에너지밴드 다이어그램에서 페르미 에너지 준위로부터 쉽게 구할 수 있음
- 공간전하분포에 대한 가정과 전계분포
- 계단 접합 근사 : n영역과 p영역의 도핑이 갑자기 변화
- 계단 공간 전하략 근사 : 공간전하영역이 갑자기 나타나고 끝남
- PN 접합의 전계 분포에 대한 고찰
- 외부 전압이 없어도, 공간전하영역 내에 전계가 존재 (내부전계)
- 전계방향은 n영역에서 p영역을 향하는 방향
- 공간전하분포에서 계단 접합 근사, 계단 공간 전하량 근사를 사용할 경우, 전계는 위치에 대한 선형 함수
- 전위에 대한 고찰
- 외부 전압이 없어도, 공간전하영역 내에 전위차가 존재
- n영역이 p영역보다 높은 전위
- 공간전하분포에서 계딴 접합 근사, 계단 공간 전하량 근사를 사용할 경우 전위는 위치에 대한 이차함수
- pn 접합 위치에서 내부 최대전위차 = 내부전위장벽
- 전위의 형태는 에너지 밴드 다이어그램의 상하반전
[7️⃣ PN 정션 2]
📝 역방향 인가 바이어스
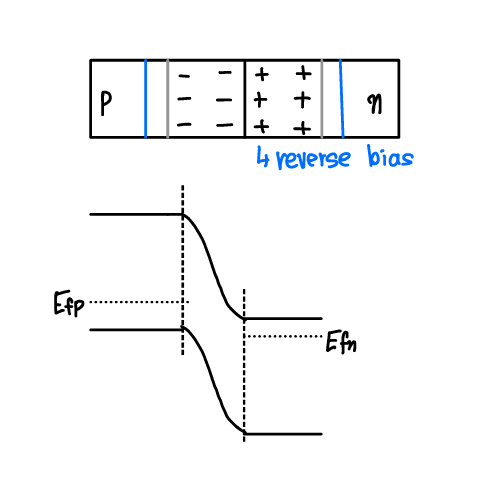
- 역방향 외부전위 인가
- pn 접합에 외부 전위를 인가하면, 시스템은 평형상태를 벗어남 → 페르미 에너지는 시스템에 걸쳐 일정하지 않음
- p형 영역을 (+) 기준으로 pn 접합에 역방향 전위를 인가하면, 양의 전위가 인가된 영역이 에너지밴드 다이어그램에서 아래쪽으로 이동
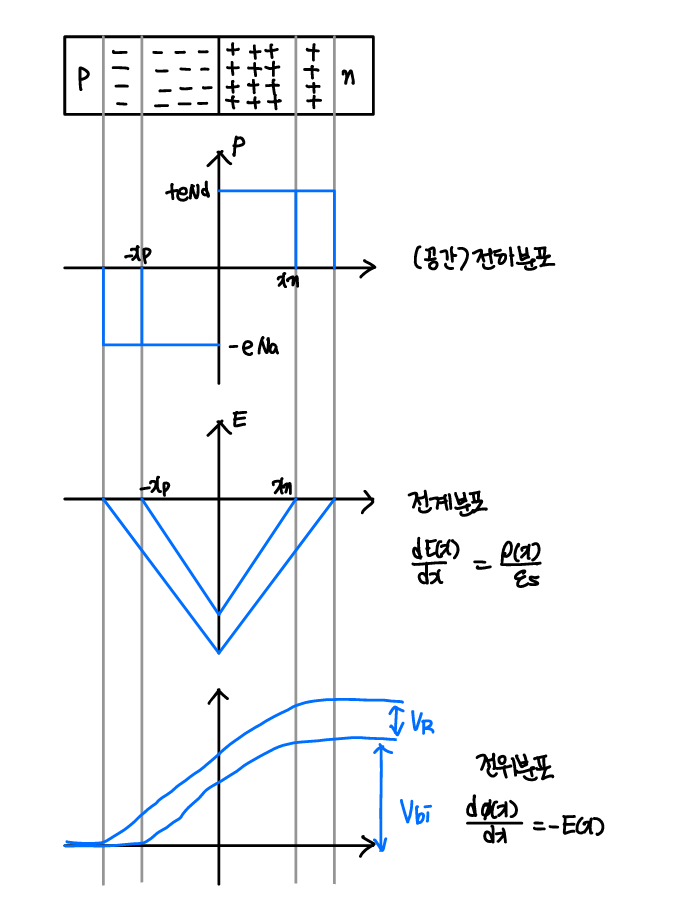
- 정성적 해석
- 역방향 인가 바이어스에 의한 전계는 pn 접합의 공간전하영역에 집중
- 이러한 전계 증가는 공간전하의 증가에 의해서만 가능하고,
- 이를 위해서는 공간전하폭의 증가를 수반함
- 캐리어 농도가 높은 n영역, p영역에는 전계가 없고, 전계가 높은 공간전하영역에는 캐리어 농도가 매우 낮으며, 캐리어 농도 구배가 높은 n/p 영역과 공간전하영역 경계에는 전기장이 확산전류를 막고 있으므로, 역방향 인가상태의 pn 접합에는 전류가 흐르지 않음.
- 공간전하의 폭
- reverse bias에서 공간전하폭이 증가한다.
- 역방향 바이어스 상태의 pn 접합은 제로 바이어스 상태와 비교하여 증가한 Vtotal = Vbi + Vr을 가지고, 공간전하폭의 증가에 기인
- 최대전계세기의 변화
- Vr이 증가하면, Emax가 증가
📝 PN 접합 커패시턴스
- 커패시턴스
- 전압 변화에 대해서 저장된 전하량 변화가 있을 때 존재
- PN 접합의 커패시턴스
- Vr의 미세변화가 있을 때, 공간전하영역에 걸리는 총 전압 변화 (Vbi + dVr)
- dVr를 발생하기 위해, 공간전하폭 증가, 공간전하 증가를 수반 → 즉, Vr에 의해서 거리 W만큼 d떨어진 위치에서 전하량 변화
📝 접합 항복
- pn 접합에 역방향 인가 전압이 증가할 때
- 낮은 Vr에서는, 전류가 흐르지 않음
- 높은 Vr에서, 결국 전류가 흐르고 경우에 따라서는 소자가 망가짐
- 높은 Vr에서 전류가 흐를 때 이를 접합항복이라고 하고, 대표적 매커니즘 2개
- 제너효과 (Zener effect) : 비파괴항복, 제너 다이오드의 원리
- p영역, n영역의 도핑농도가 모두 높을 경우 발생
- 도핑농도가 높으면 공간 전하 폭이 감소하고, 이때 높은 Vr이 걸리면, 매우 극심한 에너지 밴드 휘어짐 발생
- 이 경우, p영역의 가전자대와 n 영역의 전도대가 동일 에너지 준위에서 가까운 거리에 위치 가능
→ 터널링에 의한 전류 발생
- 애벌런치효과 (avalanche effect, 눈사태 효과) : pn 다이오드의 파괴항복
- 높은 Vr에 의해 높은 공간전하영역 전계(E) 발생
- 공간 전하 내 전자, 정공이 크게 가속되어 격자의 원자와 충돌 시, 새로운 전자-정공 쌍 생성
- 새로 생성된 전자-정공 쌍을 포함해 가속되어 새 전자-정공 쌍 생성
- 전자-정공 쌍이 눈사태처럼 갈수록 증가하여, 전류증가
[8️⃣ PN 정션 3]
📝 순방향 인가 바이어스
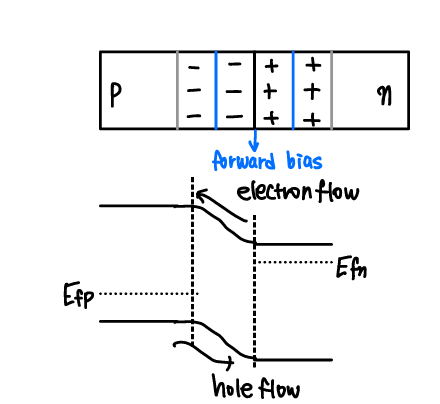
- 순방향 외부전위 인가
- pn 접합에 외부 전위를 인가하면, 시스템 평형상태를 벗어남
→ 페르미 에너지는 시스템에 걸쳐 일정하지 않음 - p형 영역을 (+) 기준으로 pn접합에 순방향 전위를 인가하면, 양의 전위가 인가된 p영역이 에너지밴드 다이어그램에서 아래쪽으로 이동
- pn 접합에 외부 전위를 인가하면, 시스템 평형상태를 벗어남
- 정성적 해석
- 총 전위장벽이 내부전위장벽 이하로 감소 (Vtotal = Vbi - Va)
← 공간전하폭과 공간전하영역의 전계세기 감소 - 제로바이어스 상태에서 확산전류를 막고 있던 전계세기가 감소하므로,
- 정공확산 : p영역 → n영역
- 전자확산 : n영역 → p영역
- p영역에서 n영역으로 확산된 정공과 n영역에서 p영역으로 확산된 전자는, 각 영역에서 소수캐리어에 해당
→ 각 영역은 비평형 상태
- 총 전위장벽이 내부전위장벽 이하로 감소 (Vtotal = Vbi - Va)
- 순방향 전류-전압 관계 유도를 위한 가정
- 계단형 공핍층 증가
- 맥스웰-볼츠만 근사
- 저-수준 주입 조건
- 총 전류를 모든 pn구조에 걸쳐서 일정, 각각의 전자·정공 전류는 pn 구조에 걸쳐서 연속함수, 각각의 전자·정공 전류는 공핍영역에 걸쳐서 일정
- 순방향 전압(Va)에 의해 증가한 소수캐리어 농도의 고찰
- Va에 의해, np와 pn은 각각 np0, pn0보다 증가
- 이는 반대편의 다수캐리어의 확산이 공간전하영역을 지나온 결과
- 양측으로부터의 캐리어 주입으로 인해, 공핍영역은 유사-페르미레벨로 분리
- 그에 따라 위 두 식은 공핍영역 끝에서 소수캐리어 농도를 의미
[9️⃣ 금속-반도체 정션]
📝 금속과 반도체 에너지밴드의 에너지 정의
- 진공 준위 (vacuum level)
- 자유전자의 위치에너지
- 물질 내 전자 에너지의 기준점
- 일함수 (work function)
- 진공준위 기준으로
- 금속의 최외각 자유전자까지의 에너지 차이 (양수로 표현)
- 반도체 페르미에너지까지의 에너지 차이 (양수로 표현)
- 전자친화력 (electron affinity-function)
- 물질이 전자 하나를 얻을 때 방출하는 에너지
- 반도체의 경우는 E0 - Ec
- 이온화 에너지 (ionization energy)
- 물질에서 전자 하나를 떼어내는데 드는 에너지
- 반도체의 경우는 E0 - Ev
📝 금속-반도체 접합의 에너지밴드 다이어그램
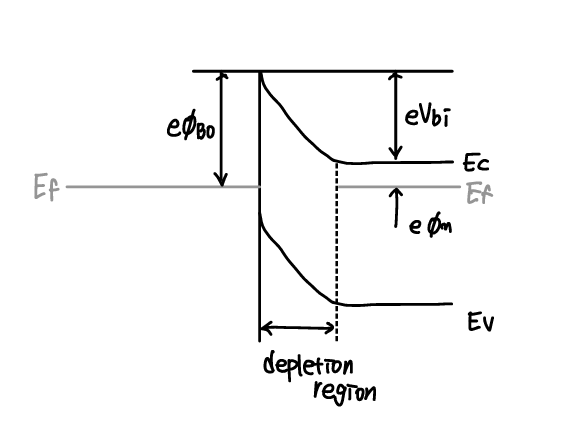
- 금속-반도체 접합의 열평형 상태 형성
- n반도체의 전자가 낮은 에너지의 금속으로 이동
(반도체의 정공이 높은 에너지의 금속으로 이동하나 소수) - n반도체의 도너 도펀트에 의한 (+) 공간전하 발생
(반대편 (-)전하는 금속/반도체 계면의 금속 쪽에 존재) - 공간전하 → 전계 → 전위가 전자의 n반도체 → 금속 이동을 방해하는 방향으로 생성
- 균형
일함수(페르미 에너지)가 동일한 에너지로 정렬 - 캐리어 이동이 가능한 열평형에서, 모든 물질의 페르미 준위는 일정
📝 금속-반도체 접합 내 에너지 장벽
- 금속-반도체 접합의 에너지 장벽
- 쇼트키 장벽 (Schottky barrier)
- 금속 → 반도체 (다수) 캐리어 이동에 대한 장벽
- 물질 고유의 특성에 기반하여, 모든 경우에 상수 (약간의 조정 가능)
- 내부전위 장벽 (built potential)
- 반도체 → 금속 (다수) 캐리어 이동에 대한 장벽
- 밴드 벤딩에 의한 장벽으로 외부 전압 등에 의해 변화
- 쇼트키 장벽 (Schottky barrier)
📝 금속-반도체 접합의 전압 인가와 전류 형성
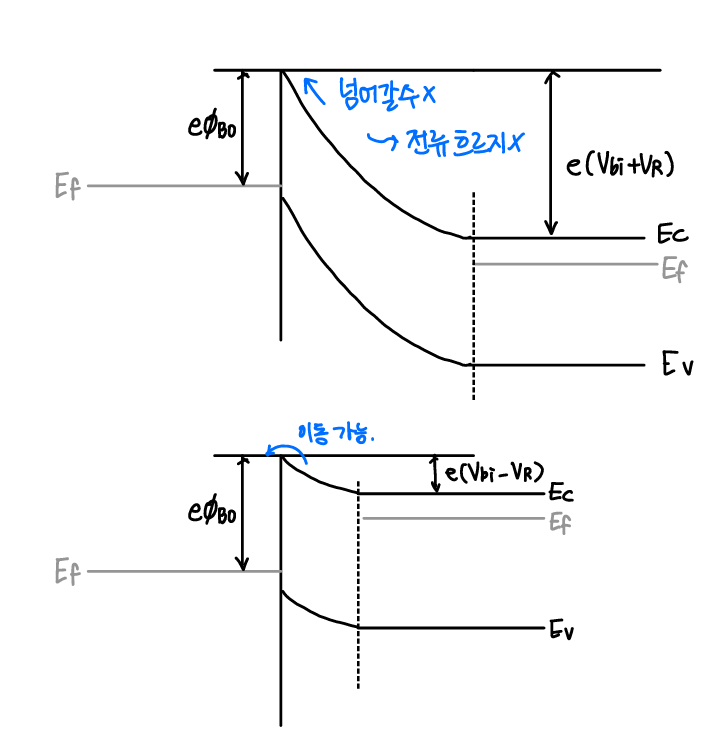
- 금속-반도체 접합의 역방향 전압인가
- 쇼트키 장벽 일정, 내부 전위 장벽 증가
- 전류 형성되지 않음
- 금속-반도체 접합의 순방향 전압 인가
- 쇼트키 장벽 일정, 내부 전위 장벽 감소
- 반도체 → 금속 캐리어 이동에 의한 전류 형성
- 반도체 → 금속 방향의 열전자 방출
: 반도체 내 다수 캐리어 중, 감소된 내부전위장벽보다 높은 열에너지를 가지는 경우 금속으로 이동 가능
📝 금속-반도체 저항성 접촉 (Ohmic contact)
- 금속-반도체 저항성 접촉 (Ohmic contact)
- 금속과 반도체 사이의 양방향 캐리어 이동에 장애(배리어)가 없는 접촉
- 반도체소자의 특성(I-V)을 소자에 연결된 금속선을 통해 외부로 뽑아내어 활용해야 하고, 이때 반도체와 금속 사이에 형성
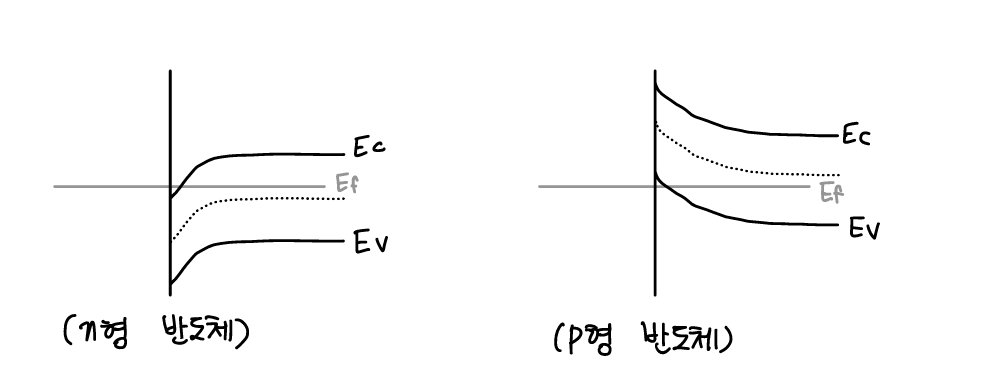
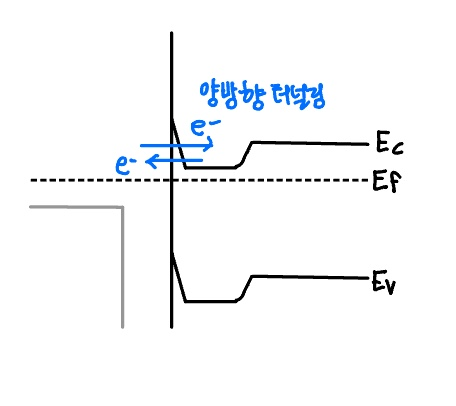
- 이상적 비정류성 장벽
- 금속의 일함수가 반도체의 다수캐리어 밴드에 주입 장벽 없이 접합될 때 형성
- 터널링 장벽
- 공간전하영역의 폭은 도핑농도의 제곱근에 반비례 (pn 접합, 금속-반도체 접합 공통)
- 금속-반도체 접합에서 반도체 도핑 농도가 매우 높은 경우
→ 수nm 수준의 매우 얇은 공간전하영역 형성
→ 터널링에 의한 원활한 캐리어 이동 가능
📝 정션에서 전류형성에 대한 고찰
- 에너지밴드 다이어그램 작성
- 금속의 일함수, 반도체의 전도대와 가전자대 에너지 준위를 변화 없이 연결
- φm, Ec, Ev는 물질 자체의 특성으로 불변 → 연결된 후 어떤 경우에도 각 물질 간 정션 장벽은 불변
- 열평형 상태 (페르미 에너지 수평) 에너지밴드 다이어그램 완성
- 0V 인가 시 총 전류 0A의 상황 (원인) 이해
- 전류의 주요 구성성분을 파악 (전자 or 정공의 드리프트 or 확산)
- 보통 다수캐리어에 의한 전류만이 주요
- 확산과 드리프트는 독립적으로 발생
(농도 구배가 있다면 확산 전류가 반드시 발생, 전기장이 있다면 드리프트 전류 반드시 발생
- 주요 구성 전류의 상호 보상에 의해 총전류 0임을 인지
- 전류의 주요 구성성분을 파악 (전자 or 정공의 드리프트 or 확산)
- 전압 방향에 따른 전류 파악
- 0V에서 전류가 발생하지 않는 원인을 고려하여, 전압 방향에 따른 원인의 해소를 해석
→ 0V, 0A의 원인이 해소되지 않거나 심화되면 전류 발생하지 않음
→ 0V, 0A의 원인이 해소되는 방향의 전압이 인가될 경우 전류 발생 - 위 전류발생 상황을 고려해 전류의 주요 성분 파악 (전자 or 정공의 드리프트 or 확산)
- 고전압이 걸리는 경우 전류 발생 매커니즘 변화 가능
- 경우에 따라,
- 한방향 전류만 발생 → 정류 접합
- 양방향 전류가 발생 → 오믹 접합, 또는 그냥 양방향 접합
- 전류 발생 X → 절연 접합
- 0V에서 전류가 발생하지 않는 원인을 고려하여, 전압 방향에 따른 원인의 해소를 해석
이렇게 해서 반도체 물성 및 소자 3편이 끝났습니다!!
이제 다음편부터는 드디어 소자에 대한 이론을 정리할 시간이네요ㅎㅎ
3편에서 끝내고 싶었지만 양이 너무 많아서 후에 제가 다시 보면서 복습할 때... 힘들겠죠...?ㅎㅎ
저는 그럼 다음 편인 반도체 물성 및 소자 4편으로 다시 돌아오겠습니다!!
다음편도 기대해주세요!😘😘😘
리드미 링크 : https://www.leadme.today/5801808498262016
김세영 님의 커리어 패스입니다. | 리드미 - LeadMe
Hy-Po 4기 A/5 김세영
www.leadme.today
(※ 본 게시물은 청년 Hy-Po 서포터즈 2기 활동의 일환으로 작성되었습니다.)
LIST
'대외활동 > SK하이닉스 청년 Hy-Po 4기' 카테고리의 다른 글
| [청년 Hy-Po 서포터즈 2기] - MISSION 05. 강의노트 작성하기 3 (반도체 공정 1편) (0) | 2024.02.13 |
|---|---|
| [청년 Hy-Po 서포터즈 2기] - MISSION 05. 강의노트 작성하기 3 (반도체 물성 및 소자 4편) (1) | 2024.02.12 |
| [청년 Hy-Po 서포터즈 2기] - MISSION 04. 자유주제 (나의 경험 공유) (1) | 2024.02.04 |
| [청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 2편) (1) | 2024.01.28 |
| [청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 1편) (1) | 2024.01.28 |



