[MISSION 02 + 서포터즈 MISSION 01. 강의노트 작성하기]
안녕하세요!
청년 Hy-Po 서포터즈 2기에 선발된 4기 교육생 김세영입니다!
오늘은 서포터즈 1번째 미션이자, Hy-Po 교육생을 대상으로 한 2번째 미션인 강의노트를 작성해보려고 합니다.
저는 청년 하이포 활동을 진행하면서 총 3가지 토끼를 잡자고 계획 했는데요.
1) 하이포 교육 내용 복습하기, 2) 운동해서 체력 기르기, 오픽과 토익을 위한 영어 공부하기가 그 3가지입니다.
아무래도 청년 Hy-Po가 SK 하이닉스라는 큰 기업에서 진행하는 활동인 만큼 하나도 놓치지 않고 공부하겠다! 라는 의지가 자연스럽게 강해지는 활동인 것 같아요.
하이포 활동이 9 to 6로 진행되는 만큼 6시에 활동이 끝나면 바로 준비해서 운동갔다가 돌아와 밥먹고 공부하려 책상에 앉으면 9시 30분 ~ 10시가 되는게 일상이네요.

사진에서 보시는 것 처럼 운동은... 거의 하루도 빠지지 않고 가려고 노력하는데요. (동아리 회의가 있는 목요일 제외) 영어 공부를 병행하는 것은 쉽지 않더군요..
다만, 활동을 진행하면서 반드시 포기하지 않아야 할 것이 바로 하이포 교육 내용 복습하기라고 생각합니다!
실제로도 꾸준히 복습을 진행하고 있었는데 이렇게 미션으로 나오게 되니 정리한 검수하며 내용들을 다시 한 번 정리하느라 애먹었네요
또한 4년차 (햇수로는 5년이지만...) 전자공학도로 회로를 그리는 건 아무래도 아이패드보다는 볼펜으로 하는 공책 필기가 훨씬 편하고 회로가 이쁘게 그려진다는 생각에 꾸준히 공책에 정리를 진행하고 있었습니다. (덕분에 시간이 몇배로 걸리는건 안비밀ㅎㅎ😅😅)




(일단 예시 사진으로 넣었는데 순서가 맞는지는 모르겠네요. 아마 안맞을듯...?)
자, 이제 그럼 제가 지금까지 정리한 회로이론 내용을 정리해볼까요?
(편의상 공책에 정리한 예제는 제외하고 이론만 정리하도록 하겠습니다!)
[1️⃣ 회로이론]
📝회로이론의 정의
- 회로이론은 전자소자(R, C, L, Tr)로 이루어진 회로망의 해석에 관한 이론
- 주로 수동소자를 기반으로 해석, 능동소자는 수동소자로 모델링하여 해석
- 회로망은 전자소자에 의해 연결되어 구성
📝회로이론 학습 목적
- 전기 및 전자 시스템의 하드웨어 구동을 위해서는 "원하는 위치에 원하는 크기와 형태의 전기 신호를 공급하기 위해" 학습
📝기본 회로 개념
- 전하 (Charge)
- 외부에서 전자기장이 가해졌을 때, 이것에 의해 영향(힘)을 받을 수 있는 입자.
- symbol : Q or q / Unit : coulomb (C)
- 가장 작은 전하량을 갖는 전하 : 전자 (-1.602 x 10^-19 C), 양성자 (1.602 x 10^-19 C)
- 전하량 보존 법칙 : 들어오는 전하량과 나가는 전하량은 같다 (전하량이 보존된다)
- 전압
- 전기적인 위치 에너지
- symbol : V / Unit : Voltage (V)
- 1V : 1C의 전하에 1J만큼의 일을 해주었을 때, 전하가 가질 수 있는 전압
- 전류
- 단위시간당 흐르는 전하의 양
- symbol : I / Unit : Ampere (A)
- 1A = 1 C/s
- 전압과 전류
- 전압과 전류는 벡터 (vector)적 성격을 지닌다. (방향)

- 전압과 전류는 벡터 (vector)적 성격을 지닌다. (방향)
- 전력(P)
- 단위시간당 전기 장치에 공급되는 전기 에너지 또는 단위 시간 동안 다른 형태의 에너지로 변환되는 전기에너지


- 에너지 (W)
- 주어진 일정 시간동안에 전달되는 총 전력
- 에너지는 전력의 시간에 대한 적분값
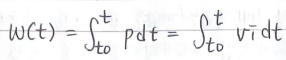
📝전압원 및 전류원
- 독립전압원
- 시간과 상관없이 일정한 전압을 공급하는 장치
- 회로에 흐르는 전류는 다른 회로 소자들에 의해 결정될 수 있음

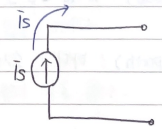
- 독립전류원
- 시간과 상관없이 일정한 전류를 공급하는 장치
- 회로에 흐르는 전압은 다른 회로 소자들에 의해 결정될 수 있음
- 종속 전원
- 이상적인 전원이지만 전원의 크기가 회로 내부의 다른 전압이나 전류에 의해 결정되는 전원
- 트랜지스터, 연산증폭기, 집적회로(Active 능동 소자)와 같은 모델을 구성

📝전류 전압 관계
- 옴의 법칙 (Ohm's law)
- 도체의 양단에 걸리는 전압은 그 도체를 통해 흐르는 전류에 직접 비례

- R이 크면 I가 작아짐
- 결국 R이 I를 방해하는 요소가 됨
- 비례상수 R을 저항이라고 하며, 단위는 옴(Ohm)
- 저항은 공급되는 에너지를 흡수하며, 이는 옴의 법칙으로 나타낼 수 있음

[2️⃣ 전압법칙과 전류법칙]
📝마디, 경로, 루프, 가지
- 마디 (node)
- 2개 또는 그 이상의 소자가 연결되는 공통 접속점
- 경로 (path)
- 마디와 소자로 구성되는 통로
- 루프 (loop)
- 경로 중에서 출발 마디와 끝나는 마디가 같은 폐경로
- 가지 (branch)
- 회로에서 단일 경로로 정의
- 하나의 소자와 그 소자의 양쪽 끝에 있는 마디로 구성
- 소자 개수로 생각하면 된다!
📝키르히호프의 전류 법칙 (KCL)
- 임의의 마디로 흘러 들어가는 전류의 대수적인 합은 0이다. (전하량 보존 법칙과 비슷한 이야기!)

📝키르히호프의 전압 법칙 (KVL)
- 임의의 폐경로에 따라 취한 전압의 대수적인 합은 0이다.

📝간단한 회로 해석 방법
- 단일루프
- 단일 루프의 경우 KVL을 통한 회로 해석이 효율적임
- 하나의 마디 쌍 (single pair node)
- 단일 루프와 짝을 이루는 회로로 한 쌍의 마디를 갖는 회로를 생각할 수 있음.
- 이러한 회로는 각 가지의 양단에 걸리는 전압이 다른 가지의 양단전압과 동일하므로 (병렬연결), KCL을 활용한 회로 해석이 효율적임
- 전원의 직렬 연결 및 병렬 연결
- 직렬 또는 병렬로 접속되어 있는 전원을 하나로 합치면 편리한 경우
- 단, 나머지 회로의 전압, 전류 및 전력 관계는 변하지 않아야 함.
- 직렬로 접속되어 있는 전압원은 각 전압원의 값을 대수적으로 합한 것과 동일한 크기의 전압을 갖는 1개의 등가전압원으로 대체 가능

- 병렬로 접속되어 있는 전류원은 각 전류원의 값을 대수적으로 합한 것과 동일한 크기의 전압을 갖는 1개의 등가전류원으로 대체 가능

- 다양한 전원 (직렬/병렬) → 하나로 합할 수 있음 (직렬 전압원 / 병렬 전류원)
- 저항의 직렬 연결 및 병렬 연결
- 직렬로 연결된 저항의 등가저항은 연결된 저항들의 대수적인 합과 동일

- 병렬로 연결된 저항의 등가저항의 역수는 연결된 저항들의 역수의 대수적인 합과 동일

- 직렬로 연결된 저항의 등가저항은 연결된 저항들의 대수적인 합과 동일
- 전압분배법칙
- 직렬로 연결된 저항에 인가된 공통 전압은 저항들에 분배가 일어남

- 직렬로 연결된 저항에 인가된 공통 전압은 저항들에 분배가 일어남
- 전류분배법칙
- 병렬로 연결된 저항에 인가된 공통 전류는 저항들에 분배가 일어남

- 병렬로 연결된 저항에 인가된 공통 전류는 저항들에 분배가 일어남
[3️⃣ 기본적인 마디해석법 및 메쉬해석법]
📝마디해석법 (nodal analysis)
- 각 마디에 전압을 할당하고 KCL 법칙을 적용함으로써 회로를 해석
- 마디해석법 간단요약
- 기준마디를 정한다. (전압은 0V로 정하기)
- 다른 마디를 정의하고 전압을 할당
- 각 마디별 KCL 방적식을 푼다
- 초마디 해석법
- 전압원이 존재하지만 이를 통하여 흐르는 전류를 정의하는 다른 방법이 없을 떄 수행하는 해석 방법
📝메쉬해석법 (mesh analysis)
- 각 메쉬에 전류를 할당하고 KVL 법칙을 적용함으로써 회로를 해석
- 메쉬
- 루프 중에서 그 내부에서 다른 루프를 포함하지 않는 루프
- 메쉬는 루프(loop)의 일종이다
- 메쉬해석법 간단요약
- 메쉬를 정의한다
- Im 정의
- 각 메쉬별 KVL 방정식 풀기
- 초메쉬 해석법
- 전류원을 공통 소자로 갖는 2개의 메쉬의 외곽 경로를 따르는 메쉬를 해석
📝마디해석법과 메쉬해석법의 비교
- 어떠한 풀이법이 회로 해석에 더 적절한 것인가?
- 더 적은 방정식을 만들어내는 풀이법
- 개인의 기호
- 어떠한 해석방법이든 상관 없다!
- 즉, "개인적으로 편한 방법을 주무기로 해석하자!"
[4️⃣ 편리한 회로 해석 기법]
📝중첩정리 (super position method)
- 모든 선형 저항성 회로망에서 어떤 저항의 양단에 걸리는 전압 또는 이에 흐르는 전류는 다른 모든 독립 전압원을 끄고 다른 모든 독립전류원을 끈 상태에서 개별전원에 의한 개개의 전압 또는 전류를 모두 대수적으로 합하여 구할 수 있음

- "선형성이 보장되는"
📝선형회로 (Linear circuit)
- Homogeneity
- 소자를 통해 흐르는 전류에 상수 k를 곱하면 소자 양단에 걸리는 동일한 상수 k를 곱한 것과 같다.

- 소자를 통해 흐르는 전류에 상수 k를 곱하면 소자 양단에 걸리는 동일한 상수 k를 곱한 것과 같다.
- Additivity
- 소자를 통해 흐르는 전류 i1(t)가 v1(t)를 생산, i2(t)가 v2(t)를 생산한다면 i1(t)+i2(t)는 v1(t)+v2(t)를 생산한다.

- 소자를 통해 흐르는 전류 i1(t)가 v1(t)를 생산, i2(t)가 v2(t)를 생산한다면 i1(t)+i2(t)는 v1(t)+v2(t)를 생산한다.
- 선형회로는 Homogeneity와 Additivity를 동시에 만족해야한다.
📝선형성과 중첩정리 증명

📝중첩정리
- 모든 선형 저항성 회로망에서 어떤 저항의 양단에 걸리는 전압 또는 이에 흐르는 전류는 다른 모든 독립전압원을 단락시키고 (끄고) 다른 모든 독립전류원을 개방시킨 (끈) 상태에서 개별 전원에 의한 개개의 전압 또는 전류를 모두 대수적으로 합하여 구할 수 있다.
- 전압원을 모두 끈다 (Short circuit)
-

-
- 전류원을 모두 끈다 (Open circuit)

📝전원변환
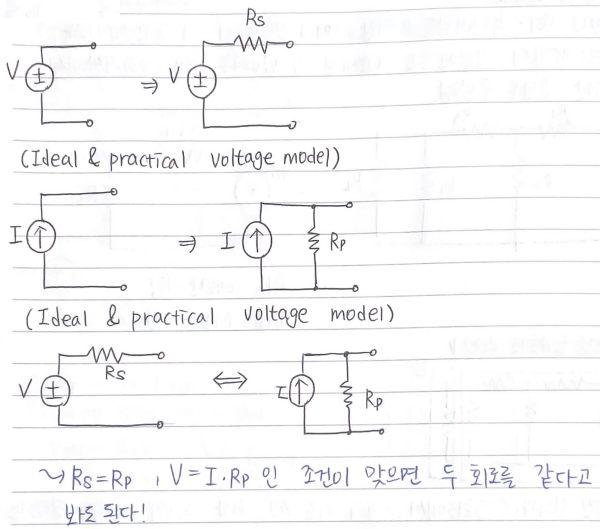
📝테브난 등가회로
- 테브난 정리
- 부하저항을 제외한 나머지 모두를 1개의 독립전압원과 1개의 저항의 직렬 연결로 대체할 수 있으며, 이때 부하저항에서 측정한 응답은 동일함

- 부하저항을 제외한 나머지 모두를 1개의 독립전압원과 1개의 저항의 직렬 연결로 대체할 수 있으며, 이때 부하저항에서 측정한 응답은 동일함
- 테브난정리 간단 요약
- 로드 저항 (관심 저항) 떼어내기
- 떼어낸 자리에 걸리는 전압 Voc (Vth) 구하기
- 내부의 모든 독립전원 off, Voc 자리에서 바라본 Req (Rth) 구하기
📝노턴 등가회로
- 노턴 정리
- 부하 저항을 제외한 회로의 나머지 모두를 1개의 독립전류원과 1개의 저항의 병렬 연결로 대체할 수 있으며, 이때 저항에서 측정한 응답은 동일함
- 노턴정리 간단 요약
- 로드 저항 제거 (short circuit 형태로 만들기)
- short 부분의 Isc (short circuit current) 구하기
- 독립 전원을 끄고, 로드 저항 부분에서 바라본 Req 구하기
📝테브난-노턴 등가회로

📝최대전력전달
- 저항 Rs와 직렬연결된 독립전압원 또는 저항 Rs와 병렬연결된 독립전류원은 RL=Rs일때 부하저항 RL에 최대전력을 전달

📝델타 - 와이 (Δ-Y) 변환

[5️⃣ 캐패시터 & 인덕터]
- DC VS AC

- 수동소자 VS 능동소자
- 수동소자 (passive)
- 공급된 에너지를 단순 소모, 저장 소자
- R, C, L
- 능동소자 (active)
- 공급된 에너지 이상으로 에너지를 증폭
- Tr
- 수동소자 (passive)
📝캐패시터 (Capacitor)
- 전기장으로 에너지를 저장하는 수동 소자
- 일반적으로 두개의 전도성 판 (plate)과 유전체 (dielectric materials & insulator)로 구성됨
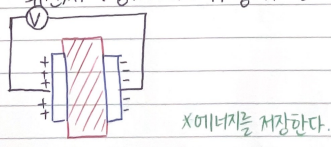
- 캐패시터의 원리
- 전압 V가 캐패시터에 인가되면, 양 판에 양전하와 음전하가 쌓이게 됨
- 이때, 양판에 저장된 전하들의 양은 같으며, 전하량은 전압과 캐패시턴스 값의 곱에 비례한
- 캐패시턴스 : 캐패시터가 전하를 저장할 수 있는 능력 (Farad(F))

- 전도성 판의 면적에 비례
- 전도성 판이 떨어진 거리에 반비례
- 유전체의 유전율에 비례
- 캐패시터의 응용
- DC 차단 / AC 통과 (필터 역할) / Shift phase / 에너지 저장 / 메모리 / 노이즈 제거
- 캐패시터의 전류 - 전압 관계
- 저장된 전하의 식을 고려하면, 캐패시터의 전류-전압 관계를 이해할 수 있음

- 캐패시터의 전력

- 캐패시터에 저장된 에너지 일

- 저장된 전하의 식을 고려하면, 캐패시터의 전류-전압 관계를 이해할 수 있음
- 이상적인 캐패시터
- 인가된 전압이 바뀌지 않으면, 캐패시터 전류는 흐르지 않는다.
- DC 전압 상황에서의 캐패시터 내부 전류는 0이다.
- 캐패시터 내부 전압은 갑자기 바뀔 수 없으며, 캐패시터 내부에 인가된 전하는 외부 변화에 점진적으로 변화한다. (천천히 변화)
- 내부에서 에너지 소실은 없다.
- 캐패시터의 병렬 연결

- 캐패시터의 직렬 연결

📝인덕터 (Inductor)
- 자기장으로 에너지를 저장하는 수동 소자
- 일반적으로 전도성 선(wire)를 코일 형태로 감은 형태로 사용됨
- 인덕터의 원리
- 전류가 인덕터로 흐르면 되면, 자기장이 도선 주위에 시계방향으로 형성 (앙페르 오른손 나사)
- 이때, 변하는 전류에 의해서 인덕터에 유도 기전력이 형성 (패러데이 전자기 유도, 렌츠의 법칙)
- 인덕턴스 : 전류의 시간에 따른 변화율과 이로 인해 발생하는 유도 기전력의 관계 (Henry(H))

- 감은 수의 제곱에 비례
- 투자율에 비례
- 코일의 면적에 비례
- 코일 길이에 반비례
- 인덕터의 전류-전압 관계
- 저장된 전하의 식을 고려하면, 인덕터의 전류-전압 관계를 이해할 수 있음
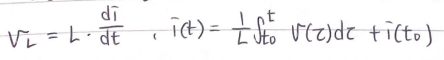
- 인덕터의 전력

- 인덕터에 저장된 에너지
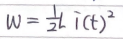
- 저장된 전하의 식을 고려하면, 인덕터의 전류-전압 관계를 이해할 수 있음
- 이상적인 인덕터
- 인덕터에 흐르는 전류가 일정하면, 내부 기전력 0
- 따라서, DC 상황에서 인덕터는 short이다. → 흐르는 전류가 없음
- 인덕터 내부 전류는 갑자기 바뀔 수 없으며, 내부에 인가된 전류는 외부 변화에 점진적으로 변화한다. (천천히 바뀐다)
- 내부에서 에너지 소실은 없다.
- 인덕터의 직렬 연결

- 인덕터의 병렬 연결

📝기초 소자들의 특성 정리

[6️⃣ RC & RL 회로]
📝circuit response (회로응답)
- 자연응답 (Natural response)
- 에너지 저장 소자 (C, L)가 포함된 회로에 전원이 없는 상태에서 회로에 나타나는 응답 특성
- 강제응답 (Forced response)
- 에너지 저장 소자 (C, L)가 포함된 회로에 초기 상태가 0인 상황에서 전원이 인가될 때 회로에 나타나는 응답 특성
- RC / RL 자연응답


- RC / RL 강제응답
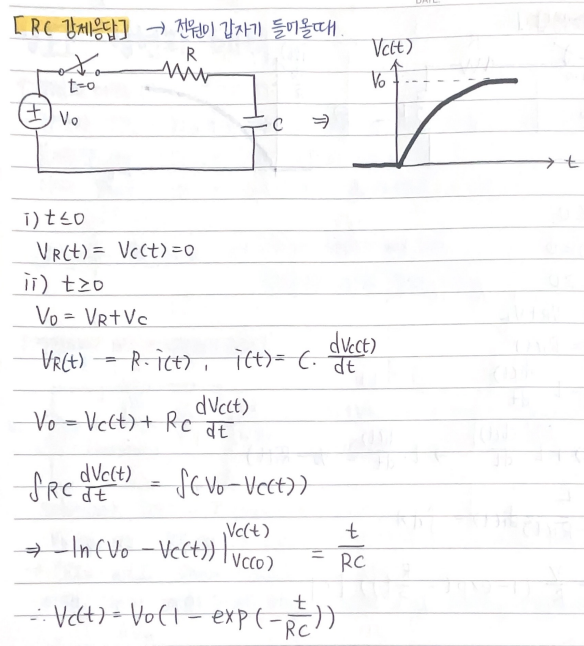

[7️⃣ 정현파 해석]
📝정현파 해석
- 정현파 전원이 회로에 인가되면, 과도 응답과 자연 응답을 배제하고, 오직 강제응답 또는 정상상태 응답을 고려할 필요가 있다
- 이때, 전원은 -∞ < t < ∞ 에 항상 존재한다고 가정함

📝정현파 해석 미분방정식 풀이

📝정현파 해석 복소 구동함수
- 관심있는 성분에 추가로 관십없는 성분을 추가해 쉽게 해석하고 나중에 관심있는 성분만 확인하자!

📝정현파 해석 복소 구동함수 풀이

이렇게 해서 하이포 4기의 첫번째 반도체 기초 과정인 회로이론 파트의 정리가 끝났습니다!
이렇게 모아두고 보니 전공생들은 1년에 걸쳐 배우는 내용을... 엄청 단기간만에 학습을 진행했네요...🙄🙄🙄
듣는 내내 복습하는 느낌으로 공부를 진행했는데요. 비전공자인 교육생 분들에게는 정말 험난한 과정이겠다고 생각을 했습니다.
함께 프로젝트를 진행하는 팀원분들 중에도 비전공자분들이 계셨는데 걱정이 필요 없을정도로 열정적으로 해줘서 너무 든든했습니다!
오히려 제가 기댈 수 있는 환경을 만들어주는 팀원분들이 너무 고마운 나날들이네요
현재는 회로이론 파트가 끝나고 난 뒤 반도체 공정 파트에 대해서도 공부했고 현재는 반도체 물성에 대해 공부하고 있습니다.
공정파트도 역시 느리더라도 천천히 복습하며 공책에다가 정리를 하고 있습니다!
공정파트의 정리 및 복습이 끝나는대로 그파트도 정리해서 올릴 생각입니다! (To be continued....)
얼른... 빠르게 진행하고 싶은 생각 뿐입니다.😭😭
이렇게 정리해두니까 뭔가 뿌듯하고 든든하네요!
전공 복습을 진행하면서 뭔가 또 새로운, 재밌는 시간이었습니다.
앞으로 배울 물성, 소자, 공정 파트에서도 열심히 공부해야겠다는 생각 뿐입니다!
그러면 이만 저는 오늘의 글을 마무리하겠습니다.
다음편으로 올라올 강의노트도 기대해주세요!🥰🥰
https://www.leadme.today/5801808498262016
(※ 본 게시물은 청년 Hy-Po 서포터즈 2기 활동의 일환으로 작성되었습니다.)
'대외활동 > SK하이닉스 청년 Hy-Po 4기' 카테고리의 다른 글
| [청년 Hy-Po 서포터즈 2기] - MISSION 04. 자유주제 (나의 경험 공유) (1) | 2024.02.04 |
|---|---|
| [청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 2편) (1) | 2024.01.28 |
| [청년 Hy-Po 서포터즈 2기] - MISSION 03. 강의노트 작성하기 2 (반도체 물성 및 소자 1편) (1) | 2024.01.28 |
| [청년 Hy-Po 서포터즈 2기] - MISSION 02. 청년 하이포리얼리즘♡ (2) | 2024.01.21 |
| SK하이닉스 청년 Hy-Po 4기 지원, 면접 후기 (1) | 2023.12.29 |



